Efficient Algorithms for Linearly Solvable Markov Decision Processes
Study of Linearly Solvable Markov Decision Processes, incorporating novel embedding techniques and scalable solutions.
As part of my Bachelor’s Thesis, I conducted in-depth research on reinforcement learning (RL) algorithms, addressing their scalability and efficiency in large and complex domains. This thesis explores the application of Linearly Solvable Markov Decision Processes (LMDPs) to tackle these challenges. A significant contribution of my work is the development of novel embedding techniques for creating precise and exact mappings between traditional MDPs and LMDPs. These techniques improve the approximation precision by 99.23% over the approach by Todorov, enabling robust and reliable comparisons across the two frameworks, regardless of the problem’s definition or the nature of its dynamics.
This research evaluates and benchmarks the performance of traditional RL models against algorithms leveraging LMDPs, such as Z-learning, within an adaptable reinforcement learning framework. By implementing scalable and efficient versions of these algorithms, I provide a comprehensive comparison that highlights the advantages of LMDP-based approaches. Additionally, the thesis delves into various factors that enhance the decision-making capabilities of RL agents, such as algorithm design and exploration strategies, demonstrating the superiority of the LMDP framework in multiple settings. Moreover, I developed an RL simulator that provides a generalized implementation of MDP and LMDP frameworks. This simulator supports optimized core methods and seamless integration with repositories like Minigrid and Gymnasium, allowing researchers to easily extend and apply it to diverse problem definitions without the need to build custom solutions.
Linearly Solvable Markov Decision Processes
LMDPs are defined as \(\mathcal{L} = (\mathcal{S}, \mathcal{S}^-, \mathcal{T}, \mathcal{P}, \mathcal{R}, \lambda)\) where:
- \(\mathcal{S}^-\): Set of non-terminal states.
- \(\mathcal{T}\): Set of terminal states.
- \(\mathcal{S}: \mathcal{S}^- \cup \mathcal{T}\): Set of states.
- \(\mathcal{P}: \mathcal{S}^- \to \Delta(\mathcal{S})\): Passive dynamics.
- \(\mathcal{R}: \mathcal{S} \to \mathbb{R}\): Reward function.
- \(\lambda\): Temperature parameter.
The optimality Bellman equation for LMDPs is:
\[\frac{1}{\lambda} v(s) = \frac{1}{\lambda} \mathcal{R}(s) + \log{\mathcal{G}_{z}(s)} - \min_{\mathbf{u} \in \mathcal{U}(s)} KL \left( \mathcal{P}_{\mathbf{u}}( \cdot | s) \bigg\Vert \frac{\mathcal{P}(\cdot | s) z(\cdot)}{\mathcal{G}_{z}(s)}\right) \quad \forall s \in \mathcal{S}^-\]where \(z(s) = e^{\frac{v(s)}{\lambda}}\) and \(\mathcal{G}_{z}(s) = \sum_{s' \in \mathcal{S}} \mathcal{P}(s' \mid s) z(s')\) with \(v(s) = \mathcal{R}(s) \quad \forall s \in \mathcal{T}\).
Using this exponential transformation, the Bellman equation can be reformulated as:
\[z(s) = e^{\mathcal{R}(s)/\lambda} \sum_{s' \in \mathcal{S}} \mathcal{P}(s' | s) z(s')\]In matrix form, this is expressed as:
\[\mathbf{z} = G\mathcal{P}\mathbf{z}\]where the vector \(\mathbf{z}\) consists of elements \(z(s)\), and the diagonal matrix \(G\) has terms \(e^{\mathcal{R}(s)/\lambda}\) on its main diagonal.
The optimally controlled transition probabilities can be obtained using the following equation:
\[\mathcal{P}_{\mathbf{u}^*}(s' | s) = \frac{\mathcal{P}(s' | s) z(s')}{\sum_{s'' \in \mathcal{S}} \mathcal{P}(s'' | s) z(s'')}\]The iterative method to solve the final matrix equation is Power Iteration, which is equivalent to Value Iteration in MDPs. However, when a model of the environment is not available, an online algorithm becomes necessary. The analogous online algorithm to Q-learning in LMDPs is Z-learning, introduced by Todorov (2006):


Methodology
Embedding Stochastic MDPs into LMDPs
The embedding of stochastic MDPs into LMDPs involves the following system of \(\vert\mathcal{A}\vert\) equations for a fixed state \(s\):
\[\begin{aligned} m_{s'} &= \log{\mathcal{P}(s' | s)} \\ b_a &= \tilde{\mathcal{R}}(s,a) + \sum_{s' \in \mathcal{S}} \tilde{\mathcal{P}}(s' | s, a) \log{\tilde{\mathcal{P}}(s' | s, a)} \\ D_{as'} &= \tilde{\mathcal{P}}(s' | s, a) \end{aligned}\]By leveraging the stochasticity of matrix \(D\) (resulting in \(D\mathbf{1} = \mathbf{1}\)), this system can be expressed in matrix form as:
\[D\left(\mathcal{R}\mathbf{1} + \mathbf{m}\right) = \mathbf{b}\]This linear system can be solved for \(\mathbf{c} = \mathcal{R}\mathbf{1} + \mathbf{m}\) using a linear solver, resulting in:
\[\mathbf{m} = \mathbf{c} - \mathcal{R}\mathbf{1}\]This formulation allows for flexibility in the choice of \(\mathcal{R}\). However, to ensure that the uncontrolled transition probabilities \(\mathcal{P}\) are normalized, we define:
\[\mathcal{R} = \log{\sum_{s' \in \mathcal{S}}e^{-c_{s'}}}\]We then find the corresponding \(\mathbf{m}\) using this normalization condition, thereby ensuring that the solution adheres to the probabilistic constraints of the LMDP framework. The entire embedding process from Todorov (2006) has been implemented in a vectorized manner, significantly enhancing the efficiency and scalability of the methodology.

Embedding Deterministic MDPs into LMDPs
When the MDP is deterministic, the previous embedding technique cannot be performed, as there is no entropy within the transition probability distribution. This makes the exact construction of an LMDP infeasible. Todorov’s approach can still be used by removing the entropy factor and scaling out the rewards when necessary, but it leads to suboptimal approximations. Therefore, an alternative methodology has been proposed in this work, presenting a novel approach for accurately and efficiently constructing the most precise possible LMDP from a deterministic MDP, outperforming previous baselines in embedding precision and robustness.
The first alternative method involves considering a stochastic “policy” to translate the MDP to an LMDP. This method results in:
\[\mathcal{R}(s) \gets \frac{1}{\left|\mathcal{A}\right|}\sum_{a \in \mathcal{A}} \tilde{\mathcal{R}}(s,a), \quad \forall s \in \mathcal{S}\] \[\mathcal{P}(s' | s) \gets \frac{1}{\left|\mathcal{A}\right|}\sum_{a \in \mathcal{A}} \tilde{\mathcal{P}}(s' | s,a), \quad \forall s \in \mathcal{S}^-, s' \in \mathcal{S}\]However, the equivalence between the MDP and LMDP rewards must consider the Kullback-Leibler’s divergence as:
\[\tilde{\mathcal{R}}(s,a) = \mathcal{R}(s) - \lambda KL \left( \mathcal{P}_{\textbf{u}} \Vert \mathcal{P} \right)\]To apply this in the desired direction, the LMDP dynamics must be known, which do not hold in this case as we are trying to construct the LMDP. An alternative method is to use the dynamics defined through the stochastic policy averaging (SPA) method, obtaining \(\mathcal{P}_{\textbf{u}}\) from these dynamics, and then updating \(\mathcal{R}\).

Initial intuition might suggest converting this into an iterative process. However, empirical experimentation across multiple settings revealed that the optimal approximation was consistently achieved in the very first iteration. Consequently, we hypothesize that there exists a factor \(K\) such that the optimal approximation of the embedded LMDP reward can be expressed as:
\[\mathcal{R}(s) = K \cdot \hat{\mathcal{R}}(s), \quad \forall s \in \mathcal{S}.\]Where \(\hat{\mathcal{R}}(s)\) is the initial approximation of \(\mathcal{R}\). The optimal value of the factor \(K\) can be determined using a search algorithm, with the objective function being the Mean Squared Error (MSE) between the value function approximation of the embedded LMDP and the original MDP. This minimization problem can be expressed as follows:
\[\begin{aligned} \min_{K \in \mathbb{R}} \quad \quad & \left\| \mathbf{v}_K - \mathbf{v}^* \right\|^2 \\ \text{subject to} \quad \quad & \mathbf{\mathcal{R}} = K \cdot \mathbf{\hat{\mathcal{R}}}, \\ & G_{ii} = e^{\mathcal{R}(s_i)/\lambda}, \quad \forall i \in \mathbb{N} \cap [1, |\mathcal{S}|], \\ & \mathbf{z}_K = G\mathcal{P}\mathbf{z}_K, \\ & \mathbf{v}_K = \lambda \log{\mathbf{z}_K}, \\ & \mathbf{v}^* = \max_{a} \left[ \tilde{\mathbf{R}}_a + \gamma \mathbf{\tilde{P}}_a \mathbf{v}^* \right]. \end{aligned}\]Binary Search (BS) can be employed to solve this minimization problem. However, although \(\mathbf{v}_K\) is a monotonically increasing function, the objective function is unimodal, making Ternary Search (TS) marginally more suitable for this problem.
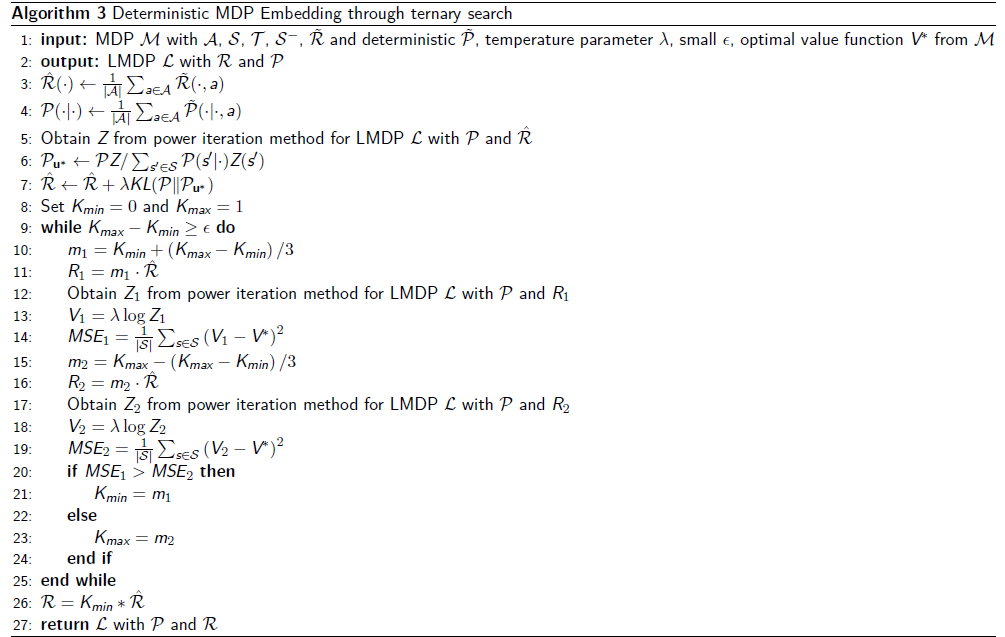
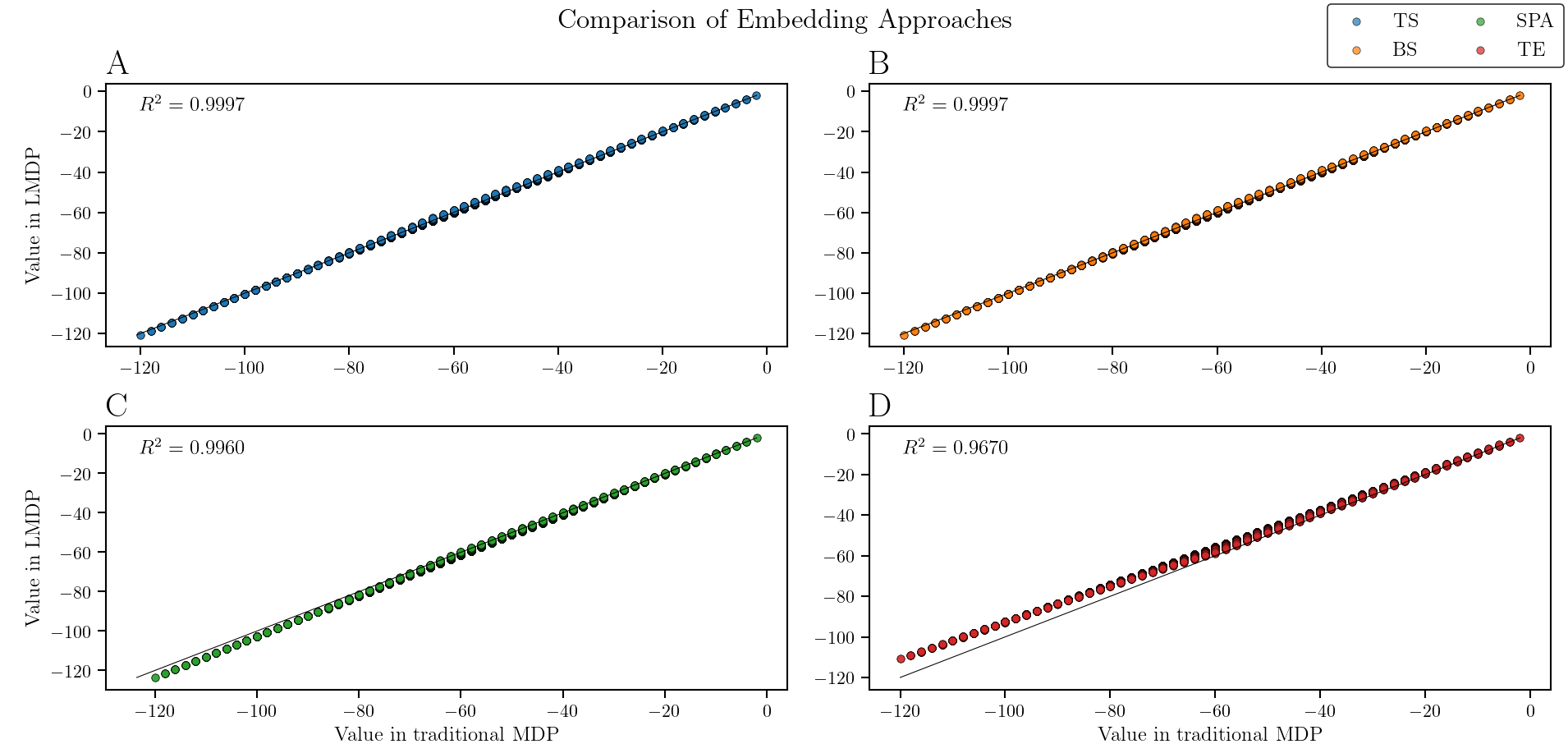
All TS, BS and SPA methods outperformed the baseline’s Todorov’s Embedding (TE) method, with TS and BS reaching the same \(R^2\), but a marginally better MSE for TS (\(0.1525\) against \(0.1527\)). TE achieved an MSE of \(19.8\), meaning our novel approach outperforms Todorov’s embedding precision for a deterministic MDP by \(99.23\%\). This difference is pronounced in larger settings, where our method still performs considerably well with an \(R^2=0.9917\) while TE decays to \(R^2=0.1996\), a significant difference. Furthermore, TS maintains consistent high precision while increasing the problem’s size, while TE’s accuracy diminishes significantly, showcasing the scalability and robustness of our method.

Experimentation
Exploration Strategies in Traditional MDPs
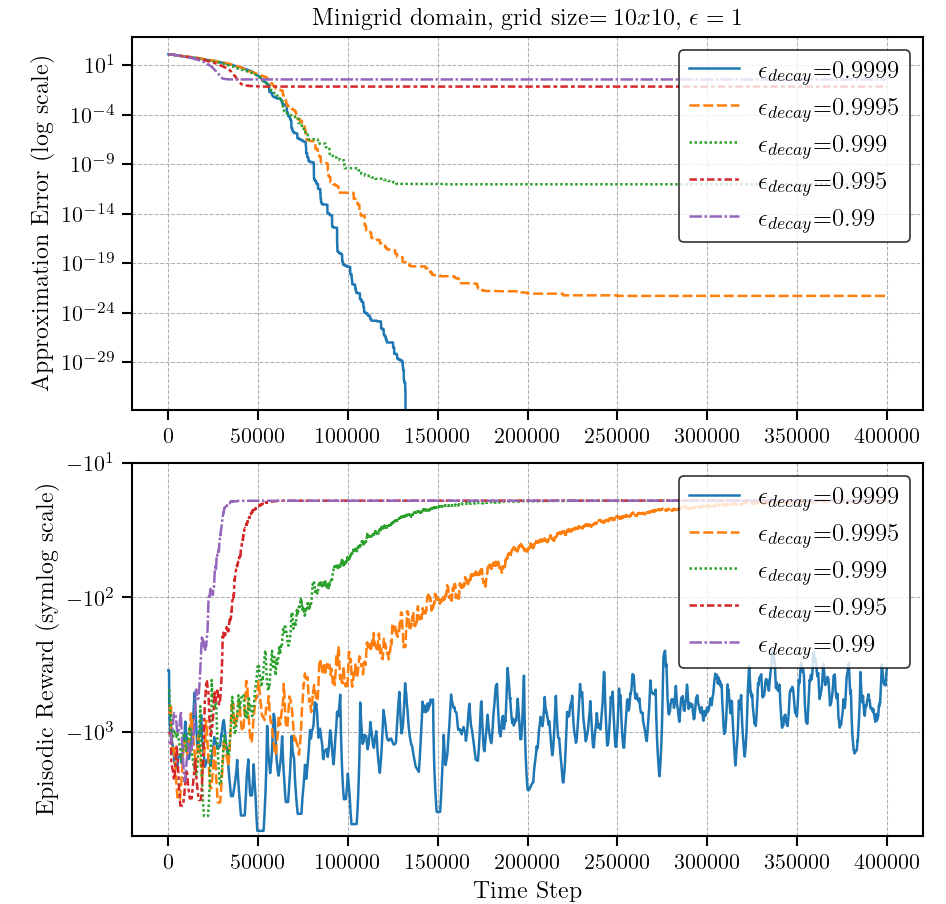
Comparative Analysis of Z-learning and Q-learning
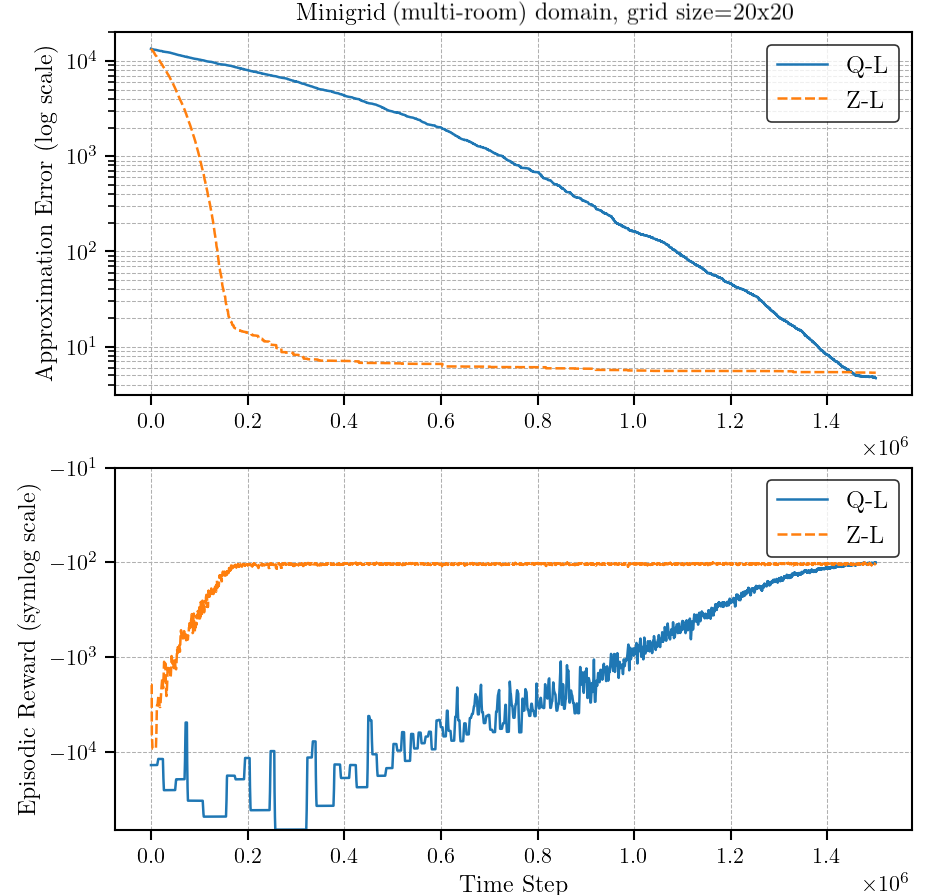
Approximation Error and Episodic Reward
Value Function and Policy Approximations
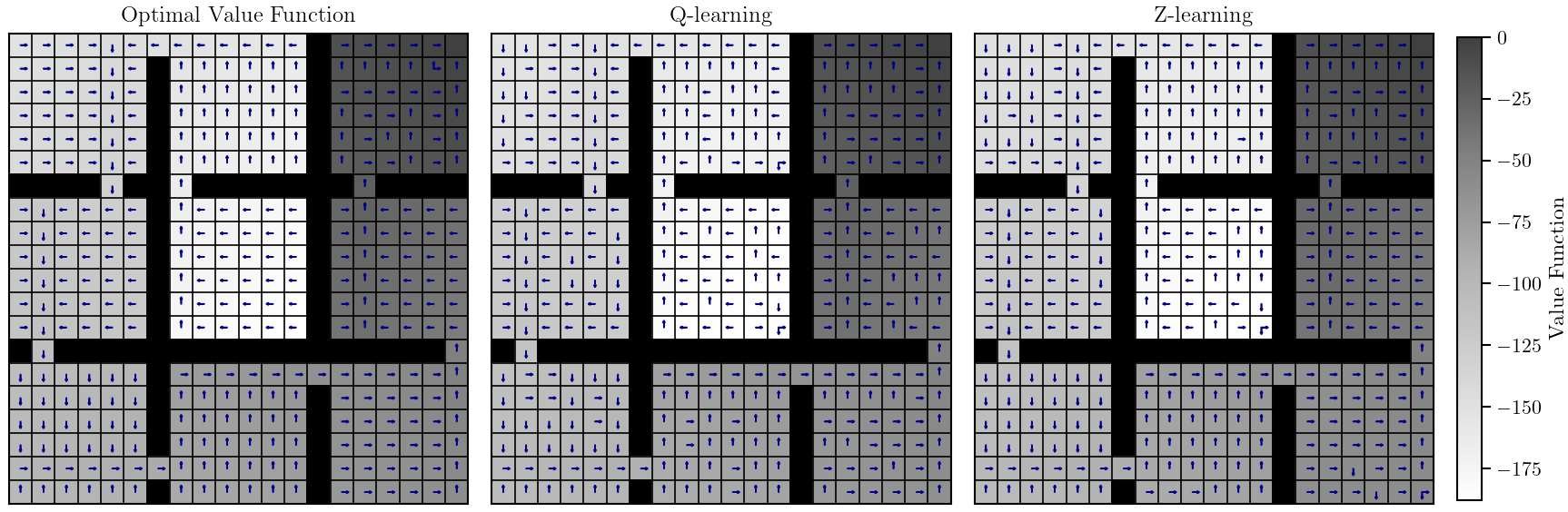
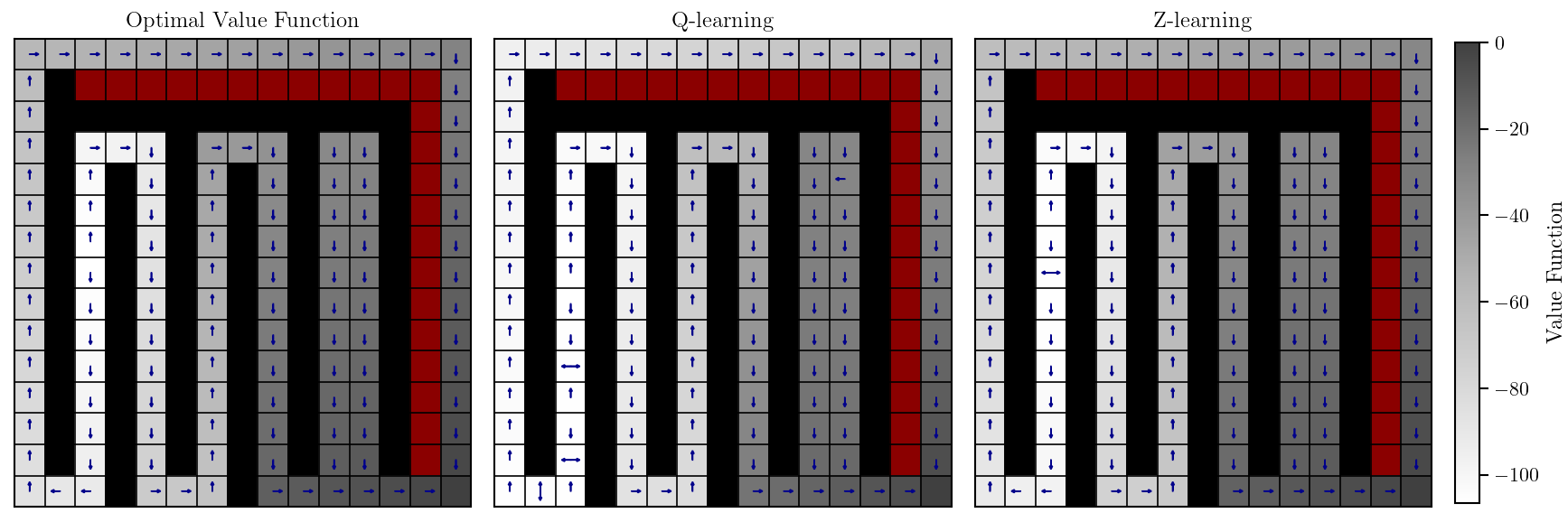
Z-learning significantly outperforms Q-learning by converging nearly 10 times faster, demonstrating superior efficiency and computational cost reduction. This efficiency is particularly notable in environments with high state-space complexity. However, inaccuracies in policy approximation for both methods arise from the lack of random sampling, as the tasks are designed to create goal-oriented problems, making random sampling impractical and less effective for these settings.
Agents Solutions
Thesis Report
Thesis presentation
References
[Gómez et al., 2014] Gómez, V., Kappen, H. J., Peters, J., and Neumann, G. (2014). Policy search for path integral control. In Calders, T., Esposito, F., Hüllermeier, E., and Meo, R., editors, Machine Learning and Knowledge Discovery in Databases, pages 482–497, Berlin, Heidelberg. Springer Berlin Heidelberg.
[Gómez et al., 2020] Gómez, V., Thijssen, S., Symington, A., Hailes, S., and Kappen, H. J. (2020). Real-time stochastic optimal control for multi-agent quadrotor systems.
[Infante et al., 2022] Infante, G., Jonsson, A., and Gómez, V. (2022). Globally optimal hierarchical reinforcement learning for linearly-solvable markov decision processes. Proceedings of the AAAI Conference on Artificial Intelligence, 36(6):6970–6977.
[Jonsson and Gómez, 2016] Jonsson, A. and Gómez, V. (2016). Hierarchical linearly-solvable markov decision problems. In Proceedings of the 26th International Conference on Automated Planning and Scheduling (ICAPS).
[Molina et al., 2023] Molina, G. I., Jonsson, A., and Gómez, V. (2023). Optimal hierarchical average-reward linearly-solvable markov decision processes. In Sixteenth European Workshop on Reinforcement Learning.
[Sutton and Barto, 2018] Sutton, R. S. and Barto, A. G. (2018). Reinforcement learning: an introduction. Adaptive computation and machine learning series. The MIT Press, Cambridge, Massachusetts, second edition.
[Todorov, 2006] Todorov, E. (2006). Linearly-solvable markov decision problems. In Schölkopf, B., Platt, J., and Hoffman, T., editors, Advances in Neural Information Processing Systems, volume 19. MIT Press.
[Todorov, 2009] Todorov, E. (2009). Efficient computation of optimal actions. Proceedings of the National Academy of Sciences of the United States of America, 106:11478–83.